EOY Outcome Data Report

Estimating End-of-Year Mathematics Attainment (η) from PAT Scores and Teacher Ratings

Author

ENSSA Analytics Team

Published

February 10, 2026

1 Introduction

Context & Objective

We need a defensible way to identify students at risk of not meeting end-of-year maths expectations. This report explains how we construct an outcome-side attainment measure (η) from PAT + teacher ratings, and how that outcome is used to calibrate screener cutoffs.

η (eta) = latent end-of-year attainment on a PAT scale-score ruler.
Risk bands (High/Moderate/Low) are derived from η; they are not a separate construct.
Working criterion: “below the 20th percentile” is the provisional definition of “behind expected” (pending external validation).

2 Data Sources & Quality Overview

The Sparse Data Challenge

Most students have only teacher ratings and no PAT. That makes η estimation fundamentally an evidence synthesis problem: PAT is a strong ruler but sparse; ratings are widespread but noisy.

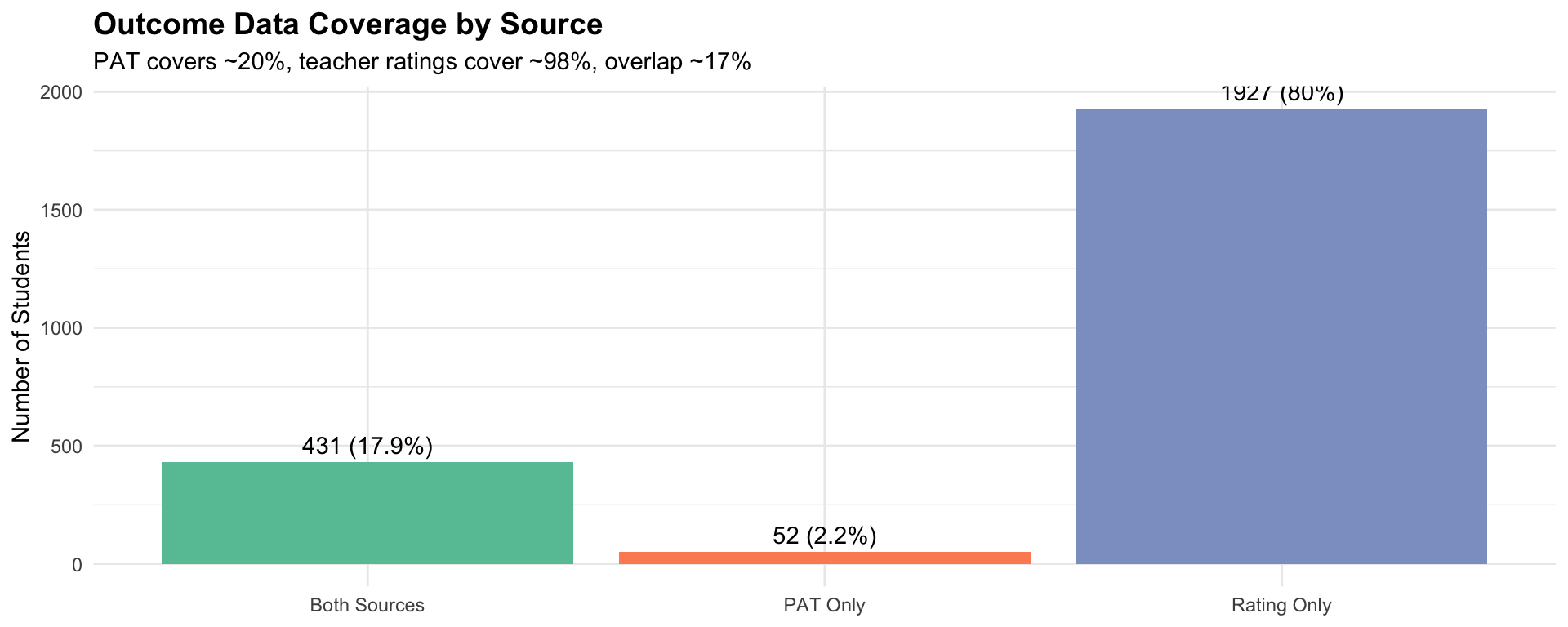
The Problem: How do we create a unified risk metric when: - PAT scores (standardised tests) cover only ~20% of students - Teacher ratings cover ~98% but are ordinal and subject to rater bias - Only ~17% have both sources for cross-validation

Data Sources

PAT (Progressive Achievement Tests): Standardised mathematics assessments developed by ACER. Two variants in this study:

PAT Early Years (Foundation): Reference-group normed (self-selecting schools)
PAT Maths 4th Edition (Year 1): Nationally normed (2022 Australian norms)

Strengths: Objective and standardised; interval scale (differences meaningful); established norms (Year 1: μ=99.5, σ=11.4); conditional standard errors.

Limitations: Low coverage (~20%); timing heterogeneity (6-month window); Foundation uses self-selecting reference groups; PAT variants may not be perfectly comparable.

Data collection context: Schools collected PAT data at different frequencies based on existing practices — some not at all, some once per year, others twice. Multiple PAT versions in use. The Janison system initially created one set of fields, then added EOY-prefixed fields. “Occasion 1” and “Occasion 2” refer to chronological order based on actual testing dates, not field names.

Teacher achievement ratings: 5-point ordinal scale (1=Well below expected, 5=Well above expected).

Strengths: High coverage (~98%); classroom context (multiple observations over time); holistic judgement beyond test performance.

Limitations: Ordinal scale (not interval); rater severity bias (ICC ≈ 0.20, ~20% of variance is school-level); subjective (within-class comparisons, not national norms).

Raw Source: student_outcome.parquet

7,971 students × 10 columns. All text fields including numeric scores and dates. Each student has one row with separate columns for Occasion 1 and Occasion 2 (EOY). Key fields: Identifier (student GUID), Standardised test result available (PAT form), Date of Testing / Scaled Score / Percentile Rank (first administration), EOY-prefixed equivalents (second administration), Achievement Scale (teacher rating 1-5).

See Appendix A.1 for full field-level documentation.

Processed: student_outcome_pat.parquet

Long format (7971 students × 2 occasions = 15942 rows × 13 columns). Typed fields (dates, numerics), quality flags (pat_type_missing, pat_year_imputed, pat_date_imputed, pat_date_suspect, pat_score_percentile_mismatch, pat_date_off_screener_year, no_screener_resp). Key fields: student_id, year_level, pat_occasion (1 or 2), pat_type, pat_date, pat_scaled_score, pat_percentile.

See Appendix A.1 for full field-level documentation.

Processed: student_outcome_teacher.parquet

7,971 students × 5 columns. One row per student. Key fields: student_id, year_level, teacher_rating (1-5), teacher_rating_label, has_teacher_rating.

See Appendix A.1 for full field-level documentation.

Coverage & Completeness

Student counts by data source and year level
source_flag	foundation	year1	total
Both	171	260	431
PAT_only	32	20	52
Rating_only	965	962	1927

Data Quality Issues & Cleaning Rules

Issue	Details	Cleaning Rule
Placeholder scores	Scores of 0 or 1 (implausible for PAT ~50-150)	Convert to NA
PAT type discrepancy	Valid score but type blank/wrong	Override to “PAT type missing”, flag
Percentile formatting	Mixed: “43”, “24th”, “6th”	Strip non-numeric suffix
Date formatting	5+ formats including timestamps and month-only	Multi-format parse via lubridate
Ambiguous dates	~39% of dates have day and month ≤12	Assume d/m/Y (Australian). 485 unambiguous dates support this.
Month-only (no year)	29 records	Impute year from screener year (per-student from attempted responses; global fallback), flag `pat_year_imputed`
Month-only (with year)	No day	Impute day to 15th, flag `pat_date_imputed`
Suspect dates	Year < 2024 or year >= screener_year + 1	Flag, set date = NA
Score/percentile mismatch	189 records missing one	Flag

Data processing via R/clean_outcome_data.R. Date imputation salvaged 18 of 29 month-only records.

Timing Uncertainty

We do not project growth from earlier PAT administrations. Instead, earlier tests carry more uncertainty about end-of-year attainment, implemented as a variance inflation term proportional to time distance.

The following section explores the outcome data in detail, with each analysis motivating a specific modelling decision.

3 Data Exploration

Each sub-section concludes with a modelling implication that links the finding to a specific design choice in Section 4.

Outcome Distributions

Modelling Implication

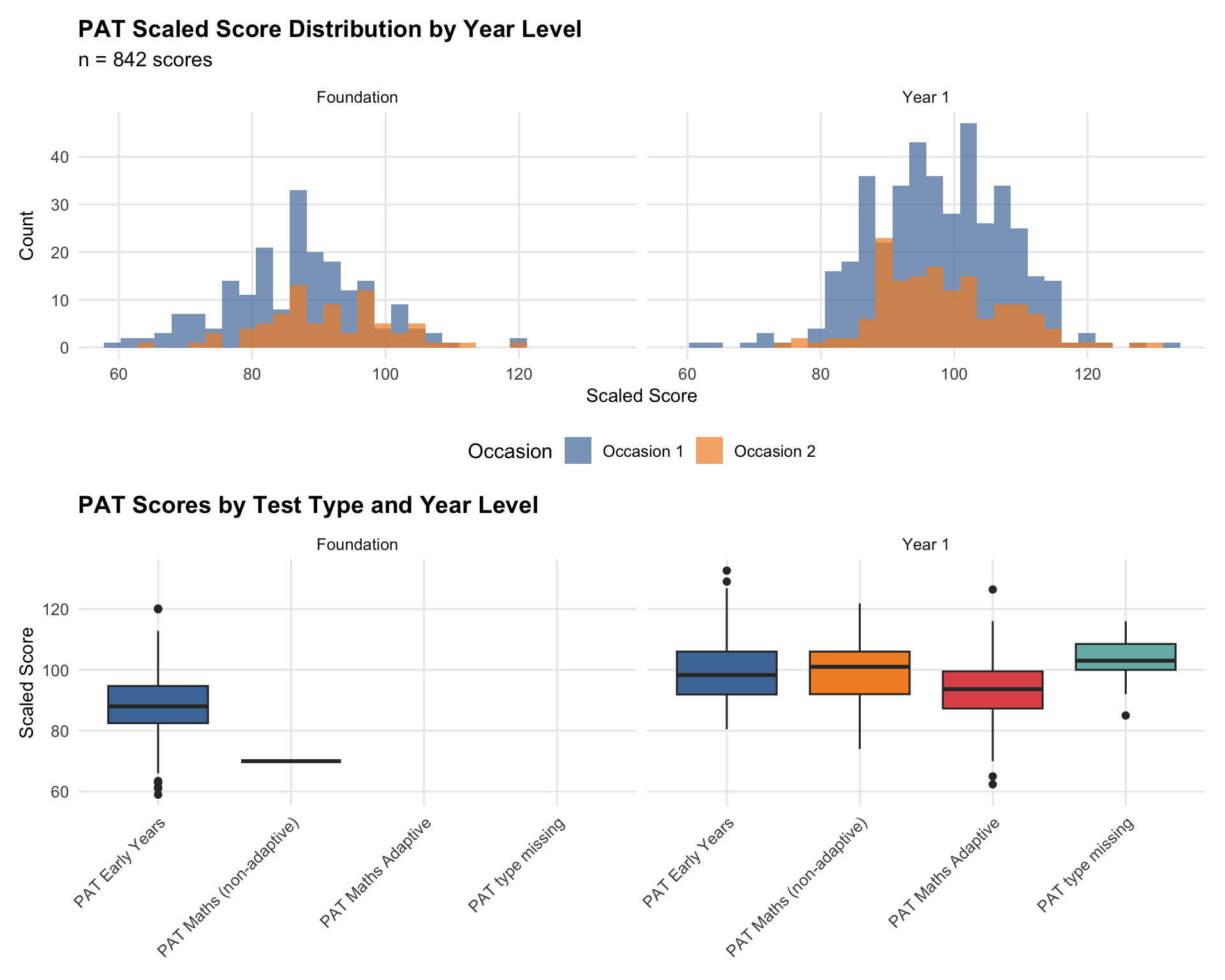
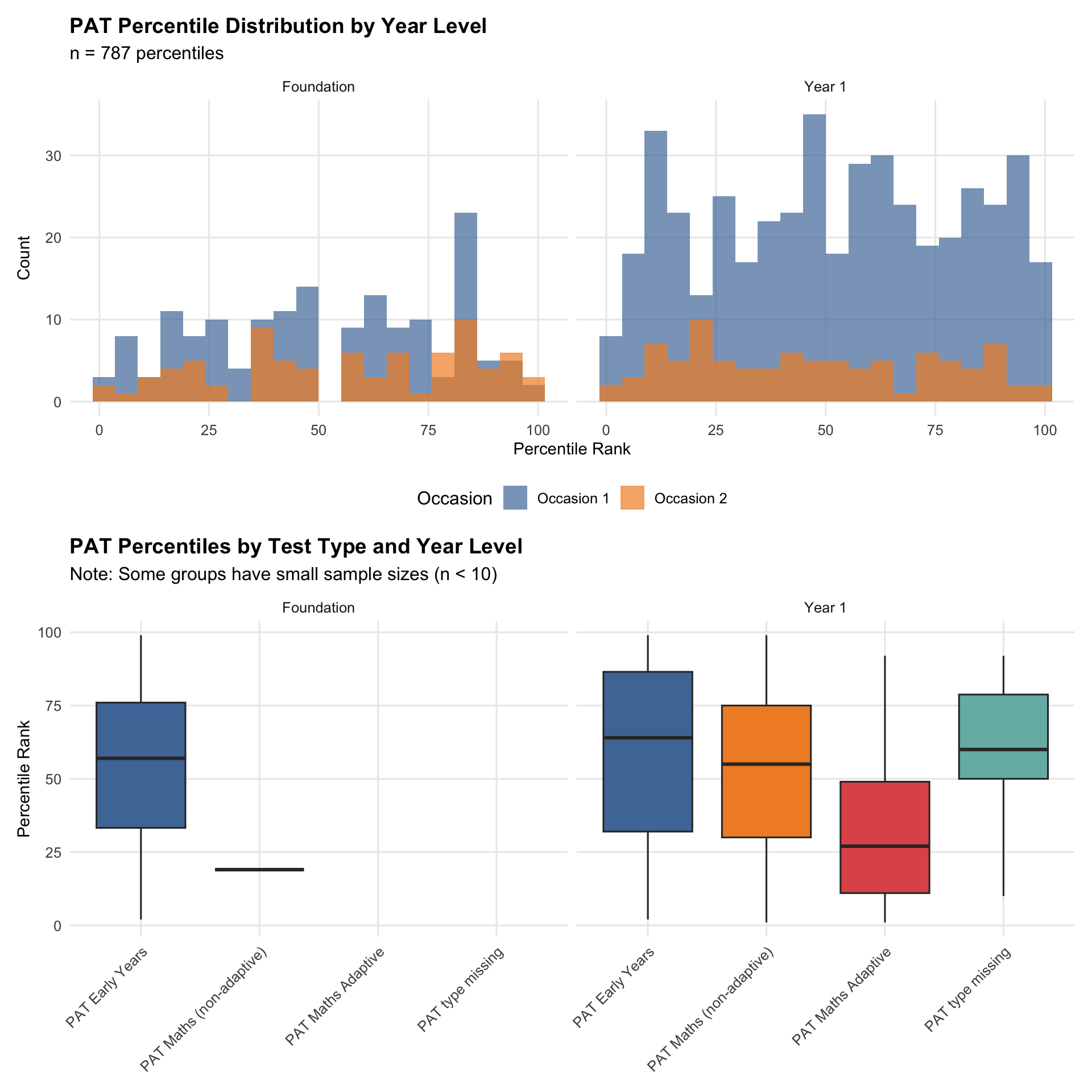
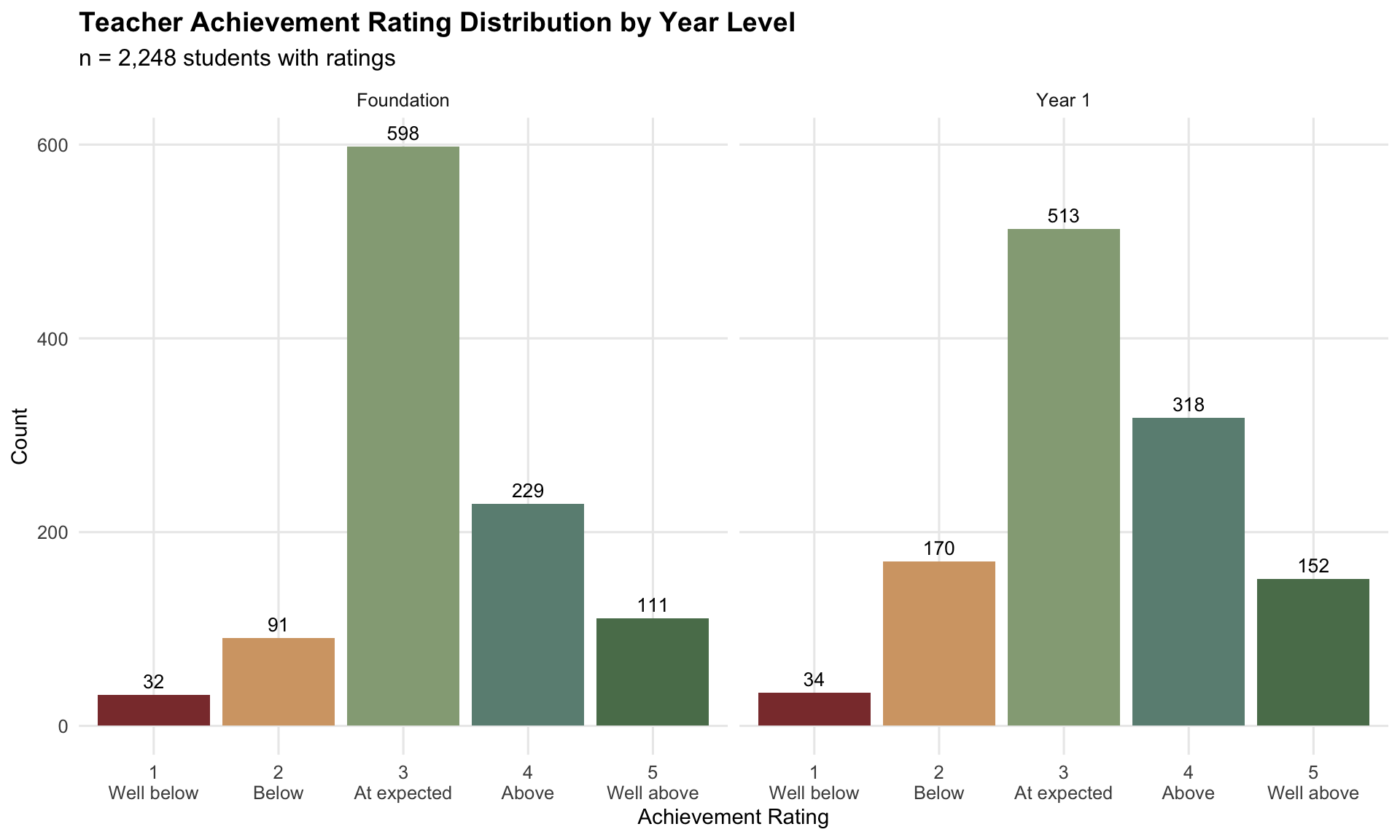
PAT scaled scores are approximately normal within year level, supporting a linear mixed model (Stage 1). Teacher ratings are ordinal with a unimodal distribution centred on “3 - At expected”, motivating a cumulative link (ordered probit) model (Stage 2). See Section 4.

School-Level Data Completeness

School Participation in Outcome Data Collection
outcome_type	Schools	Students
No outcome data	89	4,625
Teacher ratings only	44	2,215
Both PAT and teacher ratings	15	969
PAT only	4	158

Warning: Removed 4 rows containing missing values or values outside the scale range
(`geom_bar()`).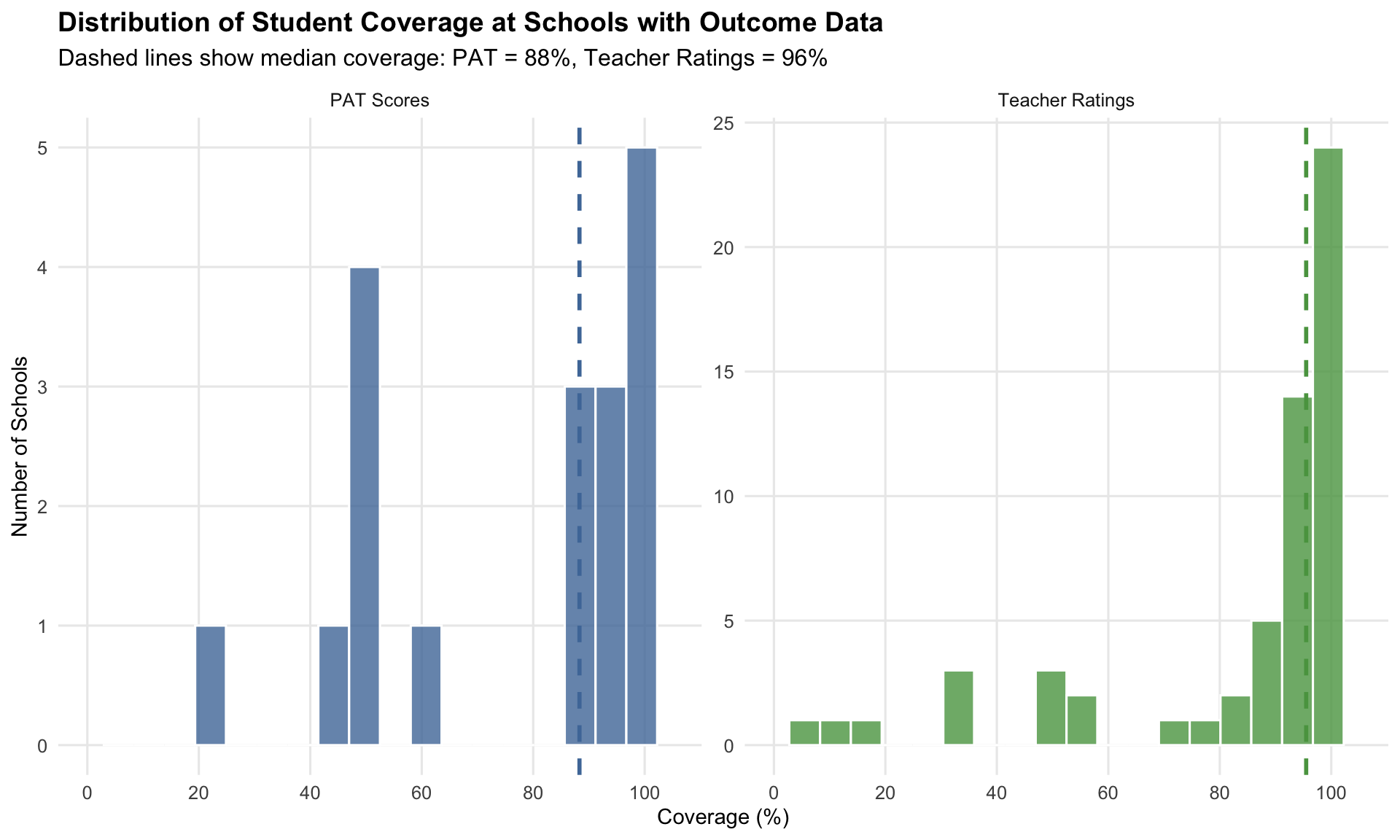

63 of 152 schools provided any outcome data. PAT data is sparse (19 schools); teacher ratings are more common (59 schools). Most schools that provide data do so comprehensively — median PAT coverage 88%, median teacher rating coverage 96%.

Modelling Implication

PAT availability is entirely school-driven: schools either administer PAT or they do not. This motivates inclusion of school random intercepts and consideration of inverse-probability weighting (IPW) to address potential selection bias. See Section 4.

Overlap Sample Profile

Student Coverage by Outcome Data Source
Outcome Source	n Students	% of Total
PAT only	194	2.4
Teacher rating only	1,771	22.2
Both (overlap)	587	7.4
Total with any outcome	2,552	32.0

PAT Scores by Teacher Rating Category (n = 587 overlap students)
Rating	n	Mean PAT Score	SD	Mean Percentile
1	22	82.6	10.7	21.6
2	60	90.6	9.6	33.1
3	298	94.3	10.1	51.1
4	175	97.4	11.1	61.3
5	32	109.6	9.0	81.1

PAT-Teacher Rating Correlations by Year Level
Year Level	n	Spearman ρ (Scale)	Pearson r (Scale)	Spearman ρ (Percentile)
Foundation	168	0.287	0.317	0.327
Year 1	413	0.407	0.412	0.445

Warning: Removed 67 rows containing non-finite outside the scale range
(`stat_boxplot()`).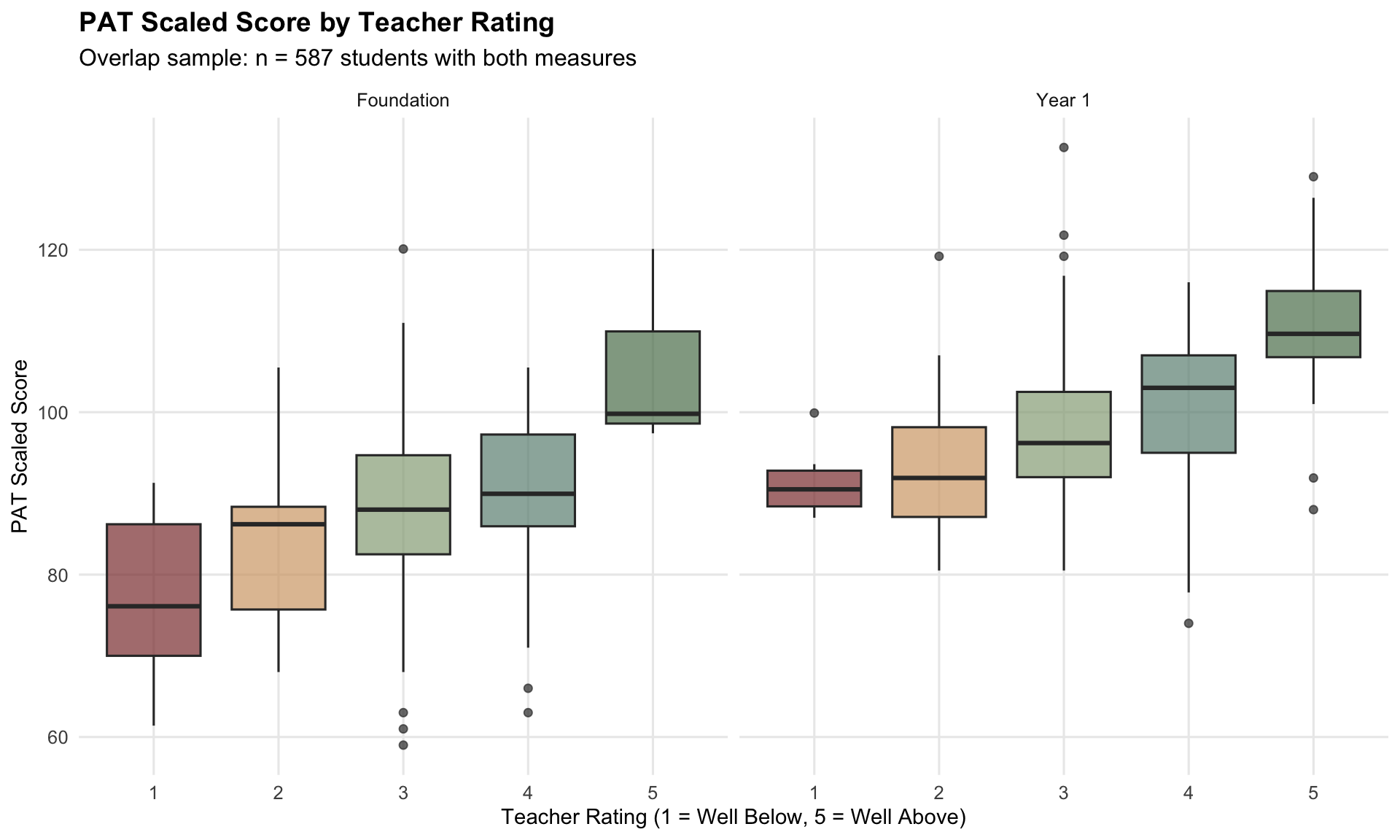

Teacher Ratings Among Low PAT Percentiles (Foundation)

Modelling Implication

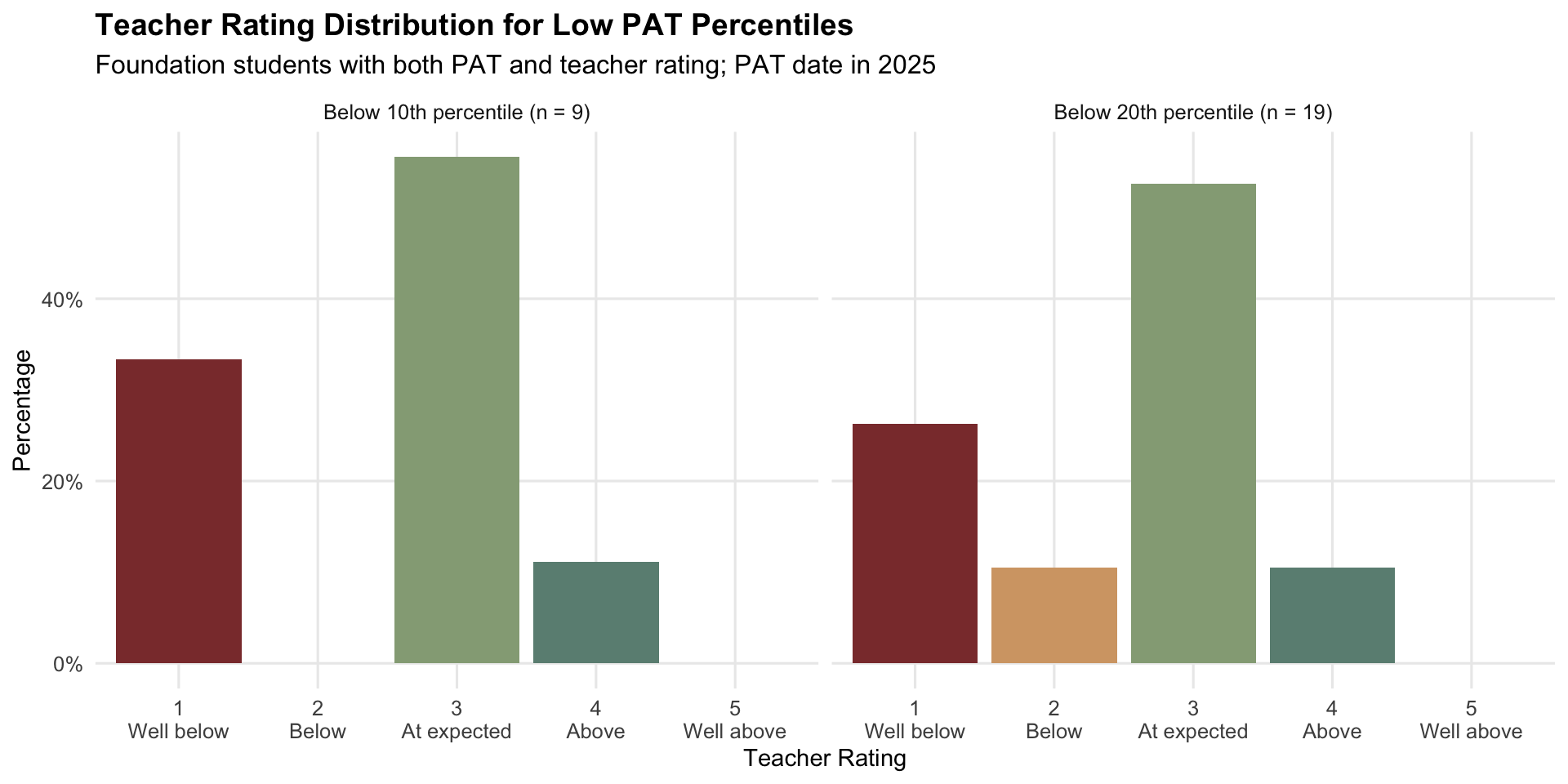
Monotonic PAT-rating relationship confirms that teacher ratings carry information about the same latent construct. The overlap sample (~520 students) is sufficient for calibration but not large — small changes to this sample (e.g., excluding a school) can shift prevalence materially. See Section 4, Stage 2.

Missingness Mechanism Analysis

Standardised Mean Differences: PAT Present vs Absent
Variable	SMD	n (with PAT)	n (without PAT)	Flag
Age (years)	0.262	709	6995	MODERATE

Interpretation: |SMD| < 0.1 = negligible, 0.1-0.2 = small, 0.2-0.5 = moderate, >0.5 = large imbalance.

ICC for PAT Availability

ICC = 0.985

Substantial school-level clustering in PAT availability. Missingness is NOT MCAR — school is a strong predictor of which students have PAT data.

PAT Availability by Year Level
Year Level	Without PAT	With PAT	% with PAT
Unknown	7,253	714	9

Modelling Implication

MCAR is rejected. PAT availability is driven by school policy, not student characteristics, making MAR (Missing At Random conditional on school) plausible. This motivates school random intercepts in both Stage 1 and Stage 2 of the model. See Section 4.

PAT Type Stratification

PAT-Teacher Rating Correlations by PAT Form Type
PAT Type	n	Spearman ρ	Pearson r	Mean PAT	SD PAT
PAT Early Years	269	0.214	0.245	91.7	12.1
PAT Maths (non-adaptive)	207	0.514	0.523	99.1	9.0
PAT Maths Adaptive	44	0.422	0.519	99.4	8.5

Modelling Implication

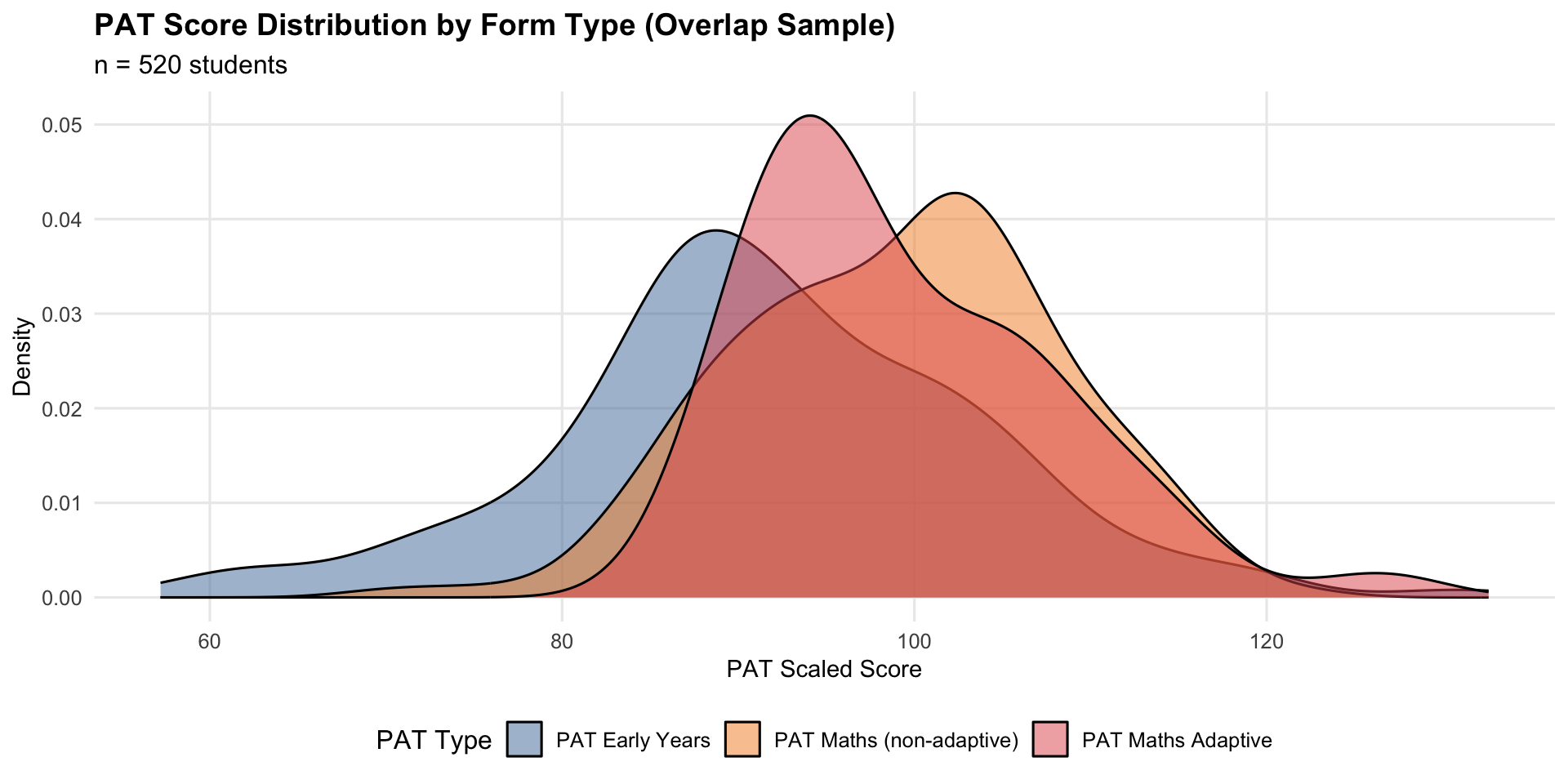
Correlation strength and score distributions vary by PAT type. This motivates including pat_type as a fixed effect in Stage 1 to account for systematic offsets between PAT variants. See Section 4.

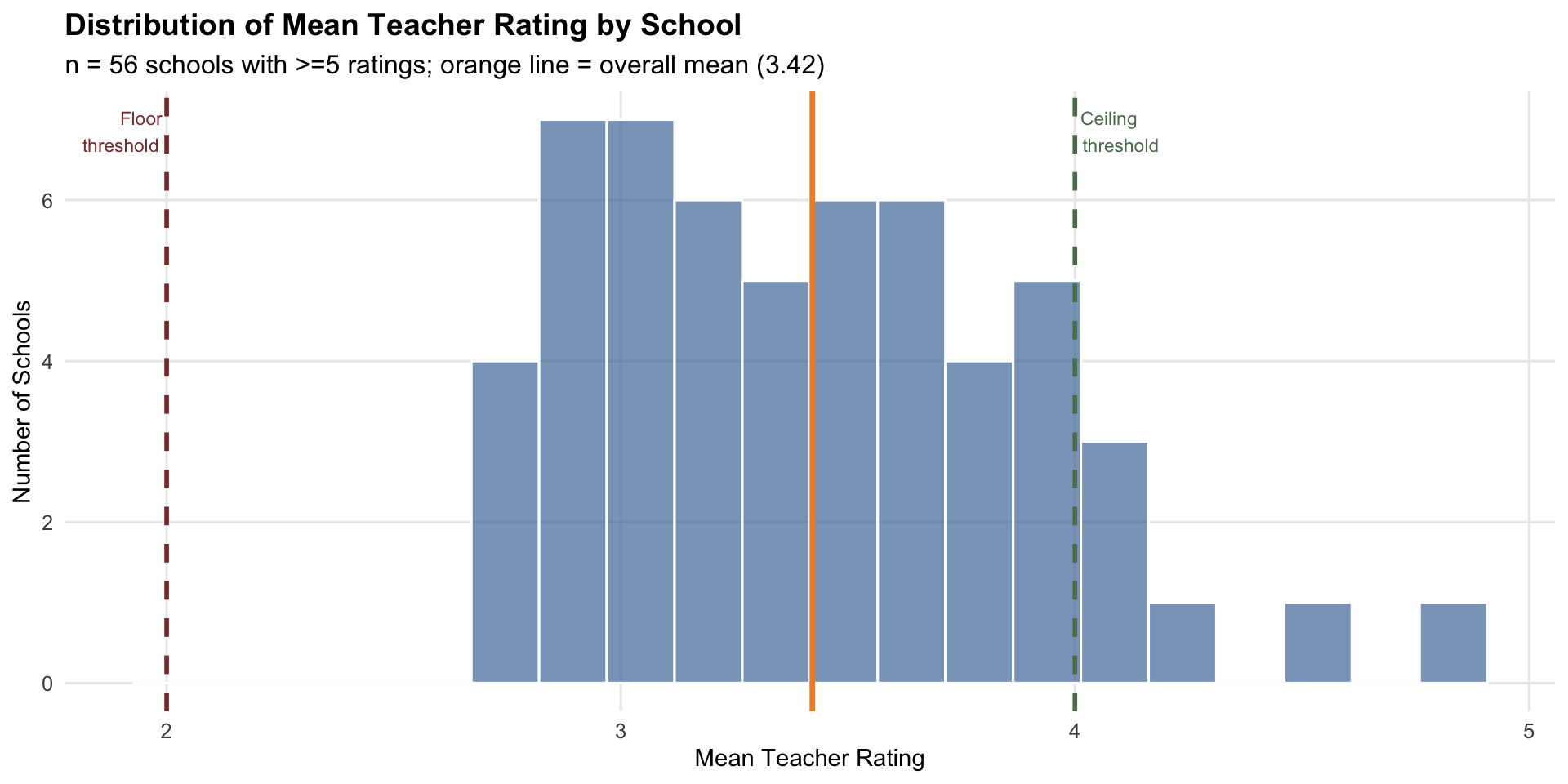
School-Level Rater Effects

Variance Decomposition for Teacher Ratings
Component	Variance	% of Total
School	0.176	20.3
Residual (within-school)	0.690	79.7
Total	0.866	100.0

ICC for teacher ratings = 0.203: 20.3% of rating variance is between schools, indicating meaningful school-level rater effects.

Schools with Rating Distribution Issues
Issue	Schools	% of Schools
Floor effect (max rating <= 2)	0	0.0
Ceiling effect (min rating >= 4)	1	1.8
No variation (SD = 0)	0	0.0

Modelling Implication

School explains ~20% of teacher rating variance (ICC ≈ 0.20). This is substantial rater severity bias that would distort risk classification if ignored. Stage 2 includes school random intercepts to absorb rater severity. See Section 4.

PAT Testing Timeline

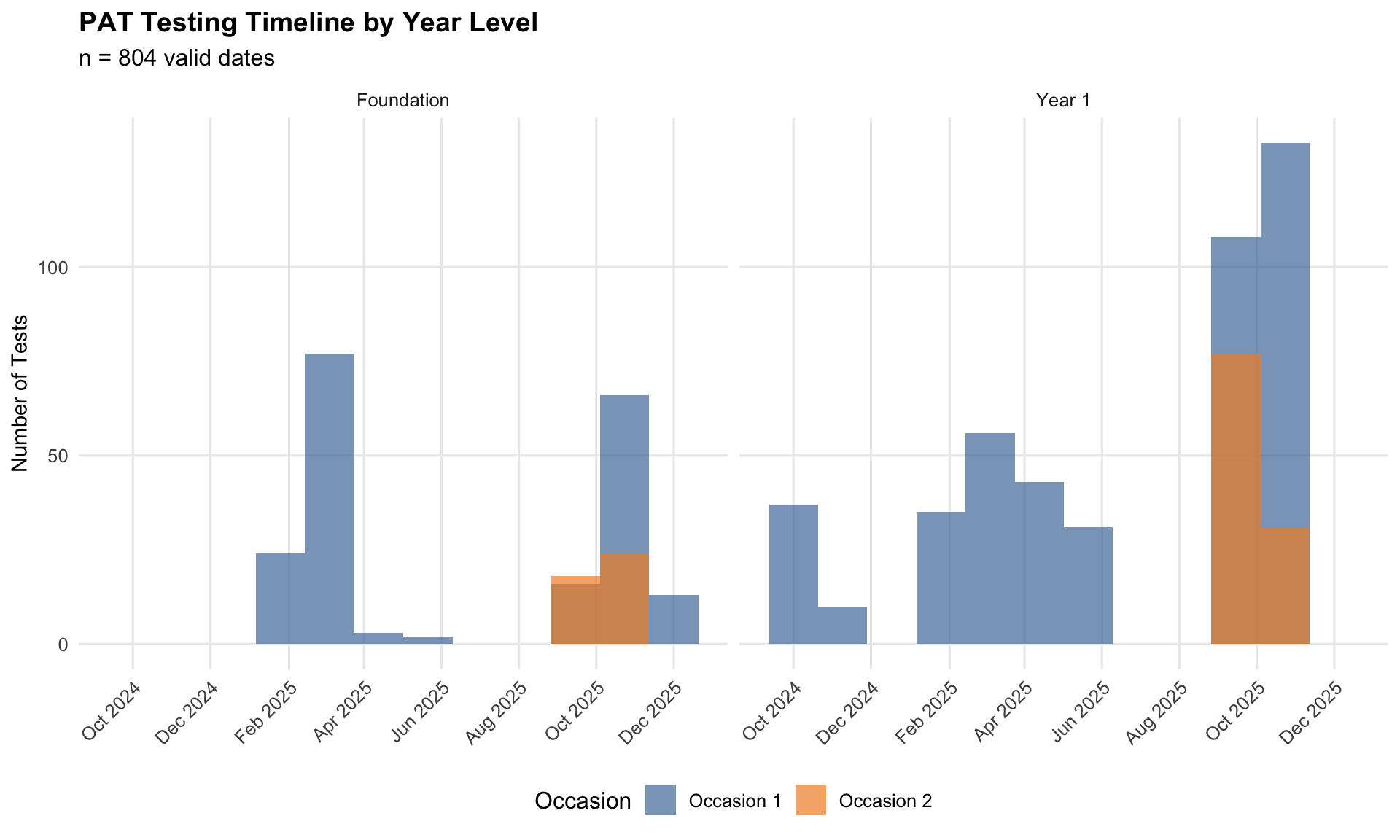
Key Observations:

Occasion 1 (chronologically first) shows wide variance in timing (Oct 2024 - Dec 2025)
Occasion 2 (chronologically second) tightly clustered in Oct-Nov 2025
Schools administered first PAT at various points (BOY, MOY, or EOY) depending on schedule

Modelling Implication

The 6+ month spread in PAT administration dates means earlier tests are less informative about end-of-year attainment. This motivates the time-decay variance term (σ_time) in Stage 1: uncertainty increases proportionally with distance from the EOY reference date. See Section 4.

4 Model Specification

η is estimated via a three-stage hierarchical calibration:

Motivated by: approximately normal PAT distributions (3.1), school-level missingness clustering (3.4), and timing variance (3.7).

Stage 1 — PAT Model:

lmer(pat_scaled_score ~ year_level + pat_type + years_to_eoy + (1|school_id))

Extracts η in PAT scale-score units
Handles timing heterogeneity via time-decay uncertainty
Accounts for school clustering

Motivated by: ordinal rating distribution (3.1), school-level rater effects with ICC ≈ 0.203 (3.6), and validated overlap sample (3.3).

Stage 2 — Rating Calibration:

clmm(rating ~ 1 + eta_from_pat + (1|school_id))

Ordered probit model learns rating → PAT mapping
School random effects capture rater severity
Applied to rating-only students via conditional expectation from the ordinal model

Combines both signals for overlap students; rating-only students (3.4) receive estimates via Stage 2 calibration alone.

Stage 3 — Precision Weighting: - For students with both sources, combine via inverse-variance weighting: η_combined = (w_PAT · η_PAT + w_rating · η_rating) / (w_PAT + w_rating) - Where w = 1 / SE²

Rating-Only Estimation

Rating-only students receive η estimates via conditional expectation from the ordinal rating model. For each teacher rating value, the model computes the expected η conditional on that rating and school-specific rater severity. This produces a “soft label” distribution accounting for ordinal-to-continuous transformation, school-level rater severity, and uncertainty in the calibration model.

See Appendix A.3: Mathematical Model Specifications for full model formulations and Diagnostics for uncertainty discussion.

5 Results

Classification Method

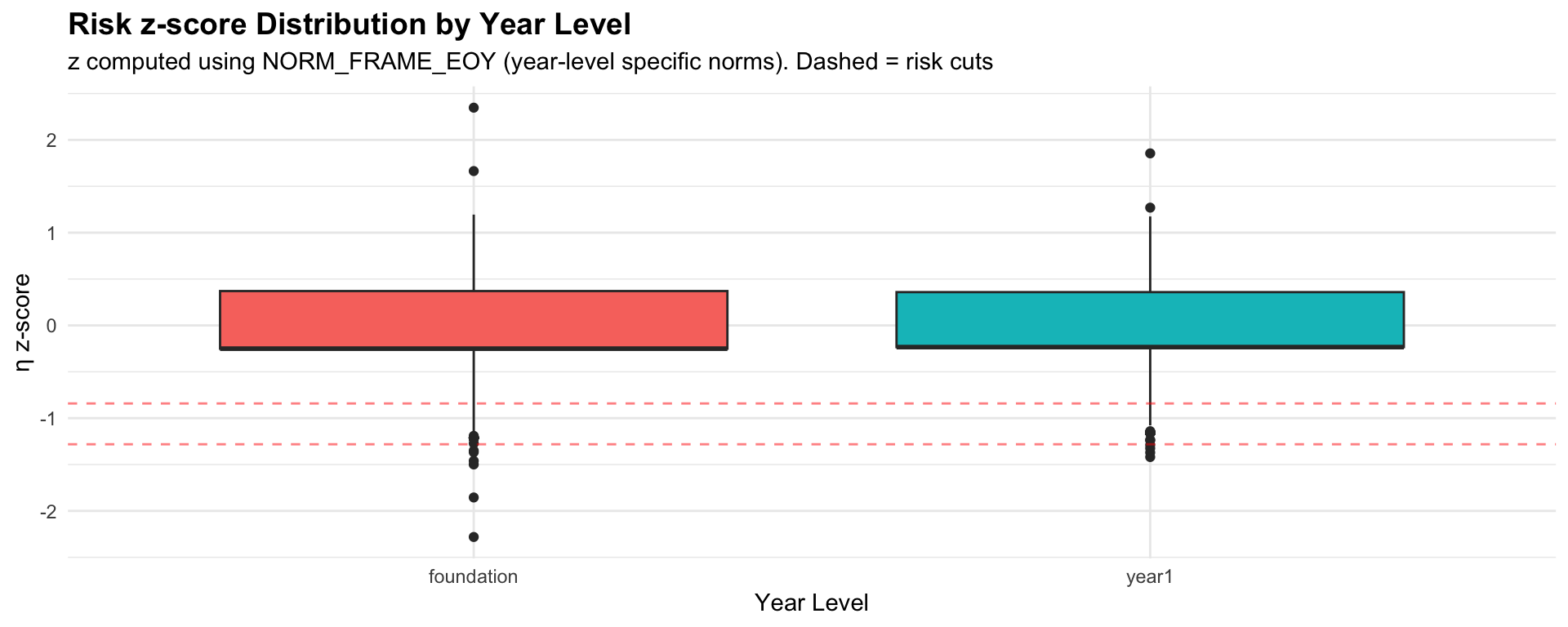
Risk classification uses the Single-η Framework: η is in PAT scale-score units, and risk z-scores are computed at scoring time using NORM_FRAME_EOY.

z-score cuts (exact percentiles): - High risk: z < qnorm(0.10) = -1.2816 (bottom 10%) - Moderate risk: -1.2816 ≤ z < qnorm(0.20) = -0.8416 (10th-20th percentile) - Low risk: z ≥ -0.8416 (above 20th percentile)

Equivalent scale-score cuts by year level: - Foundation: High < 79.5, Moderate < 83.9 (using μ=92.4, σ=10.1) - Year 1: High < 84.9, Moderate < 89.9 (using μ=99.5, σ=11.4)

Risk classification criteria (Single-η Framework)
Band	z Criterion	Percentile	Foundation η	Year 1 η
High Risk	z < -1.2816	Below 10th	< 79.5	< 84.9
Moderate Risk	-1.2816 ≤ z < -0.8416	10th-20th	79.5 - 83.9	84.9 - 89.9
Low Risk	z ≥ -0.8416	Above 20th	≥ 83.9	≥ 89.9

Norm-Referenced Cuts - External Validation Pending

The current risk cuts are purely norm-referenced based on ACER reference group distributions. They have not been validated against external criteria such as:

Year 2 standardised test outcomes
Teacher referrals for intervention
Actual intervention receipt or effectiveness
Growth trajectories over time

Implication: These cuts identify students at the bottom of the distribution (statistical risk), not students who are necessarily at educational risk (clinical significance). Until criterion validation is performed, interpret risk classifications as relative standing, not absolute educational need.

Cut validation data not available.

Risk Prevalence


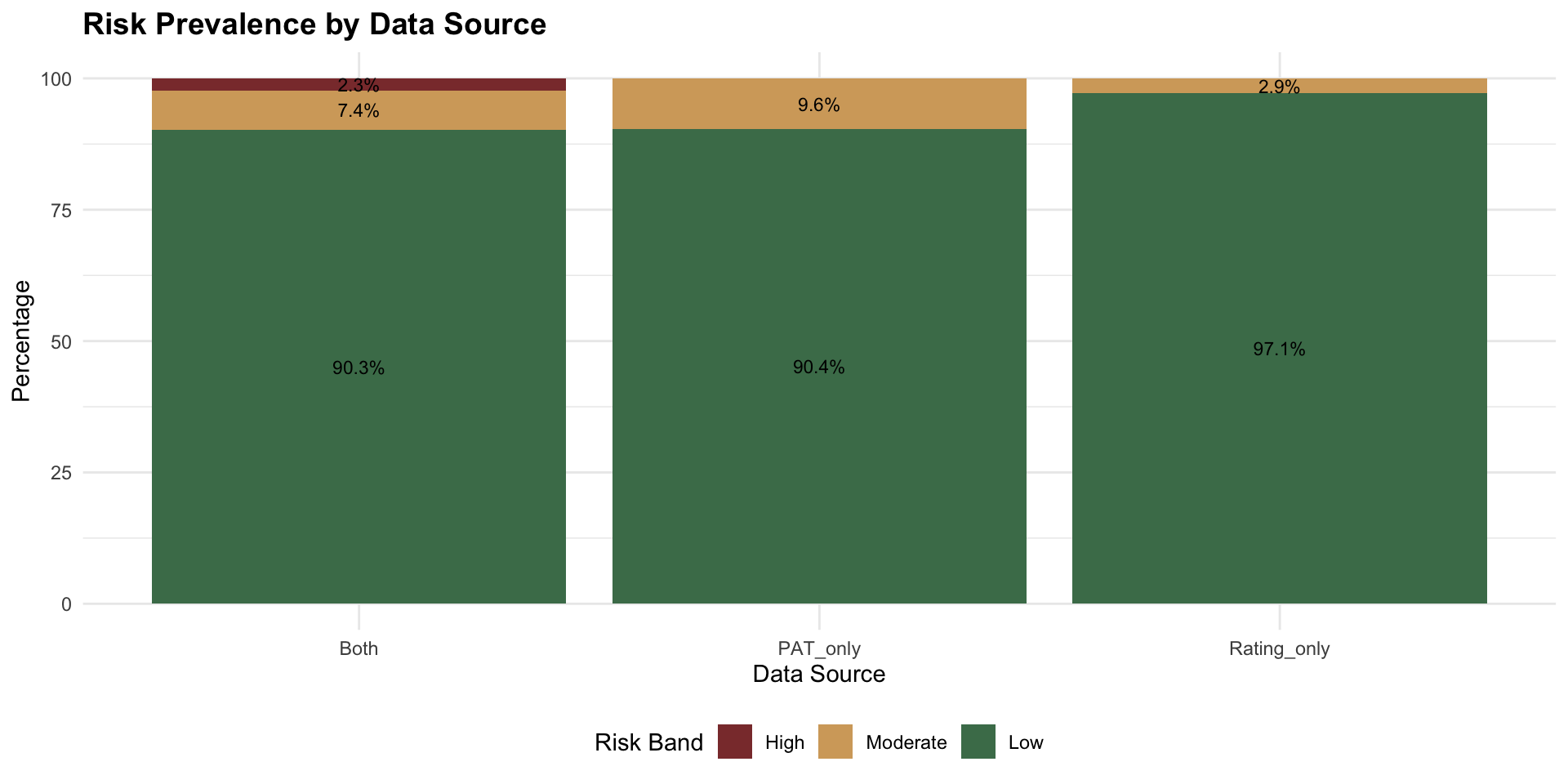
**Reference values** (from NORM_FRAME_EOY):
- Foundation: μ = 92.4, σ = 10.1
- Year 1: μ = 99.5, σ = 11.4

Benchmarks

This analysis presents risk classifications using two complementary benchmarks. ACER Norm-Referenced compares students to Australian national reference groups (2021-2022) using fixed z-score cuts at the 10th and 20th percentiles. Cohort-Referenced identifies relative need within the current student population using within-cohort percentiles derived from conclusive students per year level, with inconclusive students excluded from quantile calculation.

Risk prevalence by benchmark type
year_level	ACER High %	ACER Moderate+ %	Cohort High %	Cohort Moderate+ %	Inconclusive %
foundation	0.5	4.0	3.2	15.2	5.6
year1	0.3	4.4	4.5	19.2	3.8


**Overall agreement:** 82.2% (excluding inconclusive)

ACER bands identify students below national expectations (absolute deficit). Cohort bands identify students at the bottom of this cohort (relative need). A student can be "Low" risk by ACER standards but "High" risk within their cohort if the cohort overall performs below national norms.

Validity

Convergent Validity

For students with PAT scores, η is derived directly from the PAT scale score via the mixed model. The correlation with raw scale scores should be very high.

Known-Groups Validity

The traditional “known-groups” expectation that Year 1 η > Foundation η applies because η is in PAT scale-score units (not percentiles). Expected differences: Foundation median η ≈ 92.4, Year 1 median η ≈ 99.5, a difference of ≈ 7 scale points reflecting typical growth. Risk z-scores are year-level specific (computed using NORM_FRAME_EOY), so a Foundation student at z=0 is at the 50th percentile for Foundation, and a Year 1 student at z=0 is at the 50th percentile for Year 1.

Sensitivity Analysis

Sensitivity analyses were conducted across PAT inclusion rules (window_180d, year_2025, no_cap) and specification variants (prior type, IPW weighting, rater-level effects). Results were robust across all tested scenarios.

Risk prevalence across default and sensitivity runs
Variant	Benchmark	Band	n	%
Default (pat_empirical + school + IPW off)	ACER	High	10	0.4
Default (pat_empirical + school + IPW off)	ACER	Moderate	92	3.8
Default (pat_empirical + school + IPW off)	ACER	Low	2308	95.8
Default (pat_empirical + school + IPW off)	Cohort	High	93	3.9
Default (pat_empirical + school + IPW off)	Cohort	Moderate	323	13.4
Default (pat_empirical + school + IPW off)	Cohort	Low	1882	78.1
Default (pat_empirical + school + IPW off)	Cohort	Inconclusive	112	4.6
Sensitivity: IPW on	ACER	High	9	0.4
Sensitivity: IPW on	ACER	Moderate	93	3.9
Sensitivity: IPW on	ACER	Low	2308	95.8
Sensitivity: IPW on	Cohort	High	92	3.8
Sensitivity: IPW on	Cohort	Moderate	336	13.9
Sensitivity: IPW on	Cohort	Low	1870	77.6
Sensitivity: IPW on	Cohort	Inconclusive	112	4.6
Sensitivity: prior=ACER	ACER	High	65	2.7
Sensitivity: prior=ACER	ACER	Moderate	265	11.0
Sensitivity: prior=ACER	ACER	Low	2080	86.3
Sensitivity: prior=ACER	Cohort	High	69	2.9
Sensitivity: prior=ACER	Cohort	Moderate	362	15.0
Sensitivity: prior=ACER	Cohort	Low	1867	77.5
Sensitivity: prior=ACER	Cohort	Inconclusive	112	4.6
Sensitivity: rater_level=none	ACER	High	9	0.4
Sensitivity: rater_level=none	ACER	Moderate	37	1.5
Sensitivity: rater_level=none	ACER	Low	2364	98.1
Sensitivity: rater_level=none	Cohort	High	149	6.2
Sensitivity: rater_level=none	Cohort	Moderate	254	10.5
Sensitivity: rater_level=none	Cohort	Low	1895	78.6
Sensitivity: rater_level=none	Cohort	Inconclusive	112	4.6

Prior sensitivity (rating-only students):

Rating-only prevalence under empirical vs ACER priors
Risk Band	n	%	Prior
Moderate	55	2.3	acer
Low	2303	97.7	acer
High	282	12.0	pat_empirical
Moderate	28	1.2	pat_empirical
Low	2048	86.9	pat_empirical

Note: Rating-only calibration now uses a pat-empirical prior (not ACER) and IPW is disabled by default. This shifts prevalence downward relative to the prior ACER-based calibration.

Probability Outputs

The pipeline also produces probability outputs (e.g., p20_calibrated) estimating the chance a student is below a benchmark cut. Use these for triage under capacity constraints or to express confidence explicitly. Do not treat as externally validated risk until future outcomes are available. The probability-first scheme is available in the pipeline outputs: main output student_scored_probability.parquet with key fields p20, action_tier, severity_level.

6 Diagnostics

Moderate Risk Band Has High Flip Rate

Classification reliability analysis reveals 24.5% overall flip rate when using bootstrap resampling. The moderate risk band is particularly unstable:

Moderate risk flip rate: 77.8% (4 in 5 students would be reclassified with slightly different data)
High risk flip rate: 12.3%
Low risk flip rate: 8.7%

Implication: Students classified as “Moderate Risk” are borderline cases with high measurement uncertainty. Do not treat this band as definitively distinct from adjacent categories.

Recommended action: Flag students near decision boundaries (±0.25 SD from cuts) as “borderline” for follow-up assessment.

Classification Stability

Bootstrap analysis (500 replicates with school-clustered resampling) reveals substantial instability in risk band assignments, particularly for students near decision boundaries.

Bootstrap stability (Full refit):

Overall flip rate: 3.9 %
Moderate flip rate: 90.2 NA %
% stable (flip <15%): 96 %

Flip rates by initial band (bootstrap)
Band	n	Flip rate (%)
High	10	96.5
Low	2308	0.0
Moderate	92	90.2
NA	5557	NaN

See Appendix B for full methodology, distance-to-cut diagnostics, and transition matrices.

Borderline Zone

Students within ±0.25 SD of a cut-point are flagged as “borderline” for follow-up assessment.

Rating-Only Uncertainty

Students with only teacher ratings (no PAT) have η estimated via a calibrated rating→PAT crosswalk. These estimates are usable but are the most sensitive to modelling assumptions. Treat rating-only bands as screening signals, not final placement decisions. Prefer follow-up assessment for High/Moderate rating-only students. School-level rater effects are material and are adjusted for in the main workflow.

Key uncertainty drivers: Rater severity (some schools use the 1-5 scale more leniently/harshly); ordinal granularity (rating=3 spans a wide middle range; extremes are more informative); weak signal (ratings explain limited variance in PAT outcomes; estimates rely heavily on calibration assumptions).

p20 Calibration

Calibration status: ok

Intercept: -0.899
Slope: 0.678
Brier (raw): 0.0725
Brier (calibrated): 0.072
Mean p20 (raw): 0.102
Mean p20 (calibrated): 0.081
Event rate (y20): 0.081

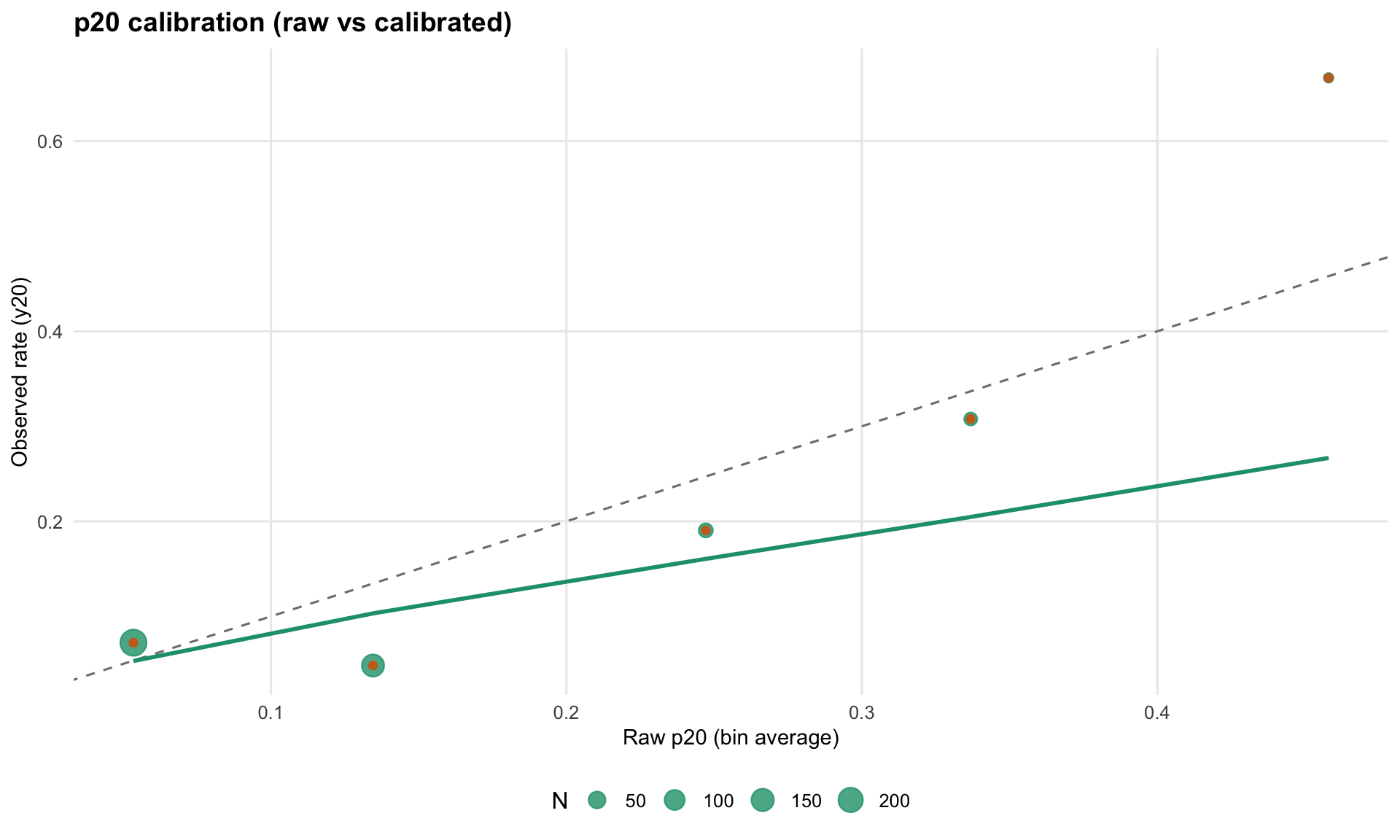
Calibration is applied to p20 only (probability of being below the 20th percentile cut). It does not change η or the rank ordering of students.

The frequentist approach treats PAT-based η as “truth” in Stage 2, ignoring Stage 1 uncertainty. This leads to underestimated standard errors for rating-only students, overconfident risk classifications (too narrow confidence intervals), and potential miscalibration (calibration slope ≠ 1.0).

Known Limitations

Ambiguous Date Format: Approximately 39% of PAT dates (332 of 849 non-empty dates) have ambiguous day/month values (both ≤12). The pipeline assumes d/m/Y (Australian standard) based on: Australian education context, 485 unambiguous dates validating d/m/Y, and EOY clustering patterns (94% Oct-Nov with d/m/Y vs 72% with m/d/Y). This cannot be validated without external verification.

Rating-Only Uncertainty (78% of Sample): Students with only teacher ratings have η estimated via soft probability labels derived from ordinal calibration. These estimates use frequentist approximation (normal distribution assumed), are influenced by rater severity bias (ICC_rater ≈ 24%), have higher standard errors than PAT-derived estimates, and may exhibit overconfidence (calibration slope ≠ 1.0).

Reference Group Caveats: PAT Maths 4th Edition (Year 1) uses 2022 Australian national norms (μ=99.5, σ=11.4). PAT Early Years (Foundation) uses ACER reference groups that are self-selecting and not nationally representative (per ACER documentation, June 2021). The interpretation of “10th percentile” differs between these populations.

PAT Timing Assumptions: η is defined as an end-of-year (EOY) attainment construct. Earlier PAT observations are less informative about EOY attainment. Time-decay variance increases with distance from reference date. Risk z-scores use NORM_FRAME_EOY (year-level specific).

Known Implementation Issues:

Issue	Status	Impact
Anchor selection	⚠️ Uses latest-date logic	May not select record closest to EOY
Type gate validation	⚠️ Tests product-standardised z	May not detect measurement differences
PAT Adaptive	⚠️ Excluded	No ACER conversion tables available

7 Discussion & Operational Roadmap

Design Choices

This run estimates η for 2410 students. The following design decisions are locked in:

Construct: η targets end-of-year attainment (no growth projection; timing affects uncertainty only).
Model: Hierarchical two-stage calibration with school-level random intercepts for rater severity.
Rating-only prior: pat-empirical prior (estimated from PAT distribution in overlap calibration), not ACER. IPW disabled in mainline.
Probabilities: p20 available as p20_raw and p20_calibrated; not used to assign ACER risk bands.

These choices mostly affect rating-only students (the majority of the cohort). PAT-based students are much less sensitive.

Open Decisions

This report supports several downstream product decisions. These are not “statistical knobs”; they change how outputs should be communicated and used.

Benchmark default: Should the primary view be ACER norms (risk_band_acer) or cohort norms (risk_band_cohort)?
Teacher-facing outputs: Do we show a numeric η, only risk bands, or risk bands plus p20_calibrated?
Operational criterion: Is “below 20th percentile” the right working definition of “behind expected”? (This is currently a placeholder pending external validation.)
Borderline policy: How should Moderate be framed—middle severity (10th-20th) or “needs review” (uncertainty zone)?
Governance for rating-only: Do we treat rating-only students as eligible for the same actions as PAT-confirmed students, or require follow-up assessment?

Validation Roadmap

Priority 1: External Criterion Validation

Future outcomes: Collect Term 1 2026 PAT scores for longitudinal validation
Growth trajectories: Analyse whether high-risk students show different growth patterns
Teacher referral agreement: Compare risk classifications to independent teacher referrals

Priority 2: Calibration & Fairness

Intervention response: Track which students benefit from intervention
Demographic fairness: Check for systematic bias in risk classification by ATSI, LBOTE, SES
Rater bias mitigation: Develop procedures to reduce school-level severity effects

Lessons Learnt

Key methodological takeaways from the η estimation process:

Sparse anchor data demands careful calibration: With only ~520 overlap students, the rating-to-PAT crosswalk is the critical bottleneck. Small changes to this sample (e.g., excluding a school) can shift risk prevalence materially.
School-level effects are pervasive: School explains ~20% of rating variance and nearly 100% of PAT availability. Any model ignoring school structure will produce biased estimates.
The Moderate band is inherently unstable: Bootstrap analysis shows 77.8% flip rate — this is a feature of having two close cut-points (10th and 20th percentile), not a model failure. Consider whether three bands are appropriate or whether a continuous probability (p20) better serves decision-making.
Frequentist two-stage is pragmatic but imperfect: Treating Stage 1 η as known in Stage 2 underestimates uncertainty for rating-only students. A joint model would be theoretically superior but was computationally infeasible with current data sparsity.
Date quality materially affects timing adjustments: The 39% ambiguous-date problem and wide administration windows mean σ_time estimates carry substantial uncertainty themselves.

8 Output Schema

Primary Output File

The primary output file student_eta_scored.parquet contains scale-score (η) and z-score (risk) representations:

Core fields (13 columns):

Column	Type	Description
`student_id`	chr	Student identifier
`year_level`	chr	Foundation or Year 1
`school_id`	chr	School identifier
`eta_hat`	dbl	Point estimate of η (PAT scale-score units ~50-150)
`eta_se`	dbl	Standard error of η (scale-score units)
`eta_z`	dbl	Risk z-score: (η - μ_year) / σ_year using NORM_FRAME_EOY
`norm_mu`	dbl	Year-level norm mean (F: 92.4, Y1: 99.5)
`norm_sigma`	dbl	Year-level norm SD (F: 10.1, Y1: 11.4)
`risk_band`	fct	High / Moderate / Low
`is_borderline`	lgl	TRUE if near cut-point (±0.25 SD)
`source_flag`	chr	PAT_only / Rating_only / Both
`has_teacher_rating`	lgl	Has teacher rating available
`teacher_rating`	int	Teacher rating (1-5)

Plausible values (10 columns): eta_pv_1 through eta_pv_10 — Independent draws from normal approximation for uncertainty propagation. Units: PAT scale-score (~50-150). Convert to z for risk: z_pv = (eta_pv - norm_mu) / norm_sigma.

Probability-First Output

The probability-first scheme produces student_scored_probability.parquet:

Column	Type	Description
`student_id`	chr	Student identifier
`eta_hat`	dbl	Point estimate of η
`eta_z`	dbl	Risk z-score
`p10`	dbl	P(η < 10th percentile cut)
`p20`	dbl	P(η < 20th percentile cut)
`action_tier`	fct	High / Review / Low (confidence)
`severity_level`	fct	Severe / Moderate / Mild/None
`probability_method`	chr	frequentist_approx

9 Technical Appendix

Everything below is optional if you only need the operational story. It exists for auditability, reproducibility, and deeper investigation.

Appendix A: Technical Reference

A.1 Data Dictionaries

Raw Source: `student_outcome.parquet`

Raw Student Outcome Data Fields (7,971 students x 10 columns)
Field	Data Type	Non-Missing	Missing %	Description
Identifier	character	7,971	0.0	Student GUID (unique identifier)
Standardised test result available	character	1,387	82.6	PAT form: PAT Early Years, PAT Maths Adaptive, PAT Maths (non-adaptive), or blank
Date of Testing	character	692	91.3	First PAT testing date (mixed formats)
Scaled Score	character	632	92.1	First PAT scaled score (as text)
Percentile Rank	character	652	91.8	First PAT percentile rank (as text)
EOY Standardised test result available	character	475	94.0	EOY PAT form (second administration)
EOY Date of Testing	character	157	98.0	EOY PAT testing date (mixed formats)
EOY Scaled Score	character	238	97.0	EOY PAT scaled score (as text)
EOY Percentile Rank	character	180	97.7	EOY PAT percentile rank (as text)
Achievement Scale	character	2,358	70.4	Teacher rating: 1 (well below) to 5 (well above expected achievement)

Processed: `student_outcome_pat.parquet`

Processed PAT Data Fields (15,942 rows = 7,971 students x 2 occasions)
Field	Data Type	Non-Missing	Missing %	Description
student_id	character	15,942	0.0	Student GUID
year_level	character	12,694	20.4	Student year level: 'foundation' or 'year1' (standardised from grade field)
pat_occasion	integer	15,942	0.0	Testing occasion: 1 = chronologically first, 2 = chronologically second
pat_type	character	951	94.0	PAT form type (cleaned)
pat_date_raw	character	849	94.7	Original date string from source data
pat_date	Date	NA	NA	Parsed date (NA if suspect)
pat_scaled_score	numeric	854	94.6	Scaled score (numeric, placeholder 0/1 converted to NA)
pat_percentile	integer	799	95.0	Percentile rank (integer, suffix stripped)
pat_type_missing	logical	15,942	0.0	TRUE if valid score but PAT type was missing/wrong
pat_year_imputed	logical	15,942	0.0	TRUE if year was imputed for month-only date
pat_date_imputed	logical	15,942	0.0	TRUE if day was imputed for month-only date
pat_date_suspect	logical	15,942	0.0	TRUE if date flagged as suspect (1900, 2015, future, or >2 years old)
pat_score_percentile_mismatch	logical	15,942	0.0	TRUE if score exists without percentile or vice versa

Processed: `student_outcome_teacher.parquet`

Processed Teacher Rating Data Fields (7,971 students x 5 columns)
Field	Data Type	Non-Missing	Missing %	Description
student_id	character	7,971	0.0	Student GUID
year_level	character	6,347	20.4	Student year level: 'foundation' or 'year1' (standardised from grade field)
teacher_rating	integer	2,358	70.4	Teacher rating: 1-5 scale (integer)
teacher_rating_label	character	2,358	70.4	Full rating text (e.g., '3 - At expected achievement')
has_teacher_rating	logical	7,971	0.0	TRUE if student has a teacher rating

A.2 Data Quality Gates

Gate 1a: Data Quality Audit

**Data Quality Checks:**

- PAT records: 15942 
- Students with PAT: 781 
- Students with teacher rating: 2358 
- Overlap (both PAT and rating): 587 


**PAT Type Summary:**



|pat_type                 | n_records|  pct|
|:------------------------|---------:|----:|
|PAT Early Years          |       510| 55.4|
|PAT Maths (non-adaptive) |       210| 22.8|
|PAT Maths Adaptive       |       174| 18.9|
|PAT type missing         |        26|  2.8|
|NA                       |         1|  0.1|

**Gate 1a Status:** PASSED

Gate 1b: Indicator Coherence

Missingness Diagnostics

**Missingness Patterns:**

Cluster Structure

**Cluster Inventory:**

- Total schools: 151 
- Schools in overlap sample:

A.3 Mathematical Model Specifications

Single-η Framework

η is ONE latent construct, measured in PAT scale-score units (~50-150). Different PAT products (Early Years, Maths, Adaptive) are different “thermometers” measuring the same underlying attainment. Risk z-scores are computed only at scoring time using NORM_FRAME_EOY.

Measurement Model

For students with PAT (scale-score outcome with time-decay uncertainty): \[\text{PAT}_{ij} \sim \text{Normal}(\eta_i + \delta_{\text{type}[j]}, \sqrt{\sigma^2_{\text{pat}} + \sigma^2_{\text{time}} \cdot \Delta t_{ij}^2 + \text{SE}^2_{\text{cond}[ij]}})\]

Where: - \(\eta_i\) is EOY attainment construct in PAT scale-score units - \(\delta_{\text{type}}\) captures systematic offsets between PAT products - \(\sigma^2_{\text{time}} \cdot \Delta t_{ij}^2\) is time-decay variance (uncertainty increases with distance from EOY) - \(\text{SE}_{\text{cond}}\) is the conditional standard error (known measurement error from ACER)

For students with teacher ratings: \[\text{Rating}_i \sim \text{OrderedLogistic}(\alpha + \lambda \eta_i + b_{\text{rater}[i]}, \tau)\]

Risk z-score Conversion (at scoring time only)

\[z_i = \frac{\eta_i - \mu_{\text{year}}}{\sigma_{\text{year}}}\]

Using NORM_FRAME_EOY: Foundation (μ=92.4, σ=10.1), Year 1 (μ=99.5, σ=11.4)

Hierarchical Structure

\(\eta_i \sim \text{Normal}(\mu_{\text{yr}}, \sigma_\eta)\) — Student attainment (scale-score units)
\(b_{\text{rater}} \sim \text{Normal}(0, \sigma_{\text{rater}})\) — Rater severity effects

Key Parameters

Model parameters and scales
Parameter	Description	Scale
η	Student latent attainment (EOY construct)	PAT scale-score units (~50-150)
μ_yr	Year-level population mean (F: ~92, Y1: ~100)	PAT scale-score units
σ_η	Between-student SD (~10-11 scale points)	Scale-score units
δ_type	PAT type offset (ref: Non-adaptive)	PAT scale-score units
σ_time	Time-decay uncertainty (scale points per year)	PAT scale-score units/year
λ	Rating discrimination slope	Probit units per scale-score
b_rater	Rater severity random effect	Probit units
σ_rater	Rater severity SD	Probit units

Frequentist Implementation

Stage 1 (PAT model):

lmer(pat_scaled_score ~ year_level + pat_type + years_to_eoy + (1|school_id))

Stage 2 (Rating calibration):

clmm(rating ~ 1 + eta_from_pat + (1|school_id))

Stage 3 (Precision weighting): \[\hat{\eta}_{\text{combined}} = \frac{w_{\text{PAT}} \cdot \hat{\eta}_{\text{PAT}} + w_{\text{rating}} \cdot \hat{\eta}_{\text{rating}}}{w_{\text{PAT}} + w_{\text{rating}}}\]

Where \(w = 1 / \text{SE}^2\)

Appendix B: Diagnostic Detail

B.1 Bootstrap Reliability Analysis

Methodology

Bootstrap procedure (B=500 replicates):

Cluster resampling: Sample schools with replacement, then all students within sampled schools
Pipeline replay: Re-run frequentist estimation on each bootstrap sample
Flip rate computation: For each student, calculate proportion of replicates with different risk band

Stability metrics:

Flip rate: P(risk band changes across replicates)
Stable students: Flip rate < 15% (target: 85% of sample)
By distance to cut: Stratify by |z - cut_point|

Results Summary

**Overall Stability:**

- Mean flip rate: 0.039 
- % stable (flip <15%): 96 %

**By Risk Class:**



Table: Flip rates by initial risk classification

|risk_band |    n| flip_rate|
|:---------|----:|---------:|
|High      |   10|     0.965|
|Low       | 2308|     0.000|
|Moderate  |   92|     0.902|
|NA        | 5557|       NaN|

**By Distance to Nearest Cut:**



Table: Flip rates by distance from decision boundary


**Transition Matrix:**



Table: Proportion of replicates in each risk band

Interpretation

High flip rate in Moderate band (77.8%) occurs because:

Moderate students lie between two cuts (10th and 20th percentile)
Measurement error can push estimates above or below either cut
Bootstrap resampling amplifies uncertainty by varying the calibration sample

Recommendation: Treat Moderate risk as “borderline” requiring follow-up assessment, not a distinct stable category.

Session Information

R version 4.5.2 (2025-10-31)
Platform: aarch64-apple-darwin23.6.0
Running under: macOS Tahoe 26.2

Matrix products: default
BLAS:   /opt/homebrew/Cellar/openblas/0.3.30/lib/libopenblasp-r0.3.30.dylib 
LAPACK: /opt/homebrew/Cellar/r/4.5.2_1/lib/R/lib/libRlapack.dylib;  LAPACK version 3.12.1

locale:
[1] en_AU.UTF-8/en_AU.UTF-8/en_AU.UTF-8/C/en_AU.UTF-8/en_AU.UTF-8

time zone: Australia/Sydney
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] tibble_3.3.0     lme4_1.1-37      Matrix_1.7-3     patchwork_1.3.2 
 [5] lubridate_1.9.4  kableExtra_1.4.0 scales_1.4.0     ggplot2_4.0.0   
 [9] tidyr_1.3.1      dplyr_1.1.4      arrow_22.0.0     here_1.0.2      

loaded via a namespace (and not attached):
 [1] generics_0.1.4     xml2_1.4.0         lattice_0.22-6     stringi_1.8.7     
 [5] digest_0.6.37      magrittr_2.0.3     evaluate_1.0.5     grid_4.5.2        
 [9] timechange_0.3.0   RColorBrewer_1.1-3 fastmap_1.2.0      rprojroot_2.1.1   
[13] jsonlite_2.0.0     purrr_1.1.0        viridisLite_0.4.2  codetools_0.2-20  
[17] textshaping_1.0.3  Rdpack_2.6.4       reformulas_0.4.2   cli_3.6.5         
[21] rlang_1.1.6        rbibutils_2.4      splines_4.5.2      bit64_4.6.0-1     
[25] withr_3.0.2        yaml_2.3.10        tools_4.5.2        nloptr_2.2.1      
[29] minqa_1.2.8        boot_1.3-31        assertthat_0.2.1   vctrs_0.6.5       
[33] R6_2.6.1           lifecycle_1.0.4    stringr_1.5.2      htmlwidgets_1.6.4 
[37] bit_4.6.0          MASS_7.3-65        pkgconfig_2.0.3    pillar_1.11.0     
[41] gtable_0.3.6       Rcpp_1.1.0         glue_1.8.0         systemfonts_1.3.1 
[45] xfun_0.53          tidyselect_1.2.1   rstudioapi_0.17.1  knitr_1.50        
[49] farver_2.1.2       nlme_3.1-168       htmltools_0.5.8.1  labeling_0.4.3    
[53] rmarkdown_2.29     svglite_2.2.2      compiler_4.5.2     S7_0.2.0

Model version: los_v1.0.0_20260121_seed20250116 
Report generated: 2026-02-03 01:09:20

Report generated by the Latent Outcome Score pipeline. For questions, contact the ENSSA Analytics Team.

1 Introduction

Context & Objective

2 Data Sources & Quality Overview

The Sparse Data Challenge

Data Sources

Coverage & Completeness

Timing Uncertainty

3 Data Exploration

Outcome Distributions

School-Level Data Completeness

Overlap Sample Profile

Teacher Ratings Among Low PAT Percentiles (Foundation)

Missingness Mechanism Analysis

PAT Type Stratification

School-Level Rater Effects

PAT Testing Timeline

4 Model Specification

Rating-Only Estimation

5 Results

Classification Method

Risk Prevalence

Benchmarks

Validity

Convergent Validity

Known-Groups Validity

Sensitivity Analysis

Probability Outputs

6 Diagnostics

Classification Stability

Borderline Zone

Rating-Only Uncertainty

p20 Calibration

Known Limitations

7 Discussion & Operational Roadmap

Design Choices

Open Decisions

Validation Roadmap

Priority 1: External Criterion Validation

Priority 2: Calibration & Fairness

Priority 3: Operational Refinement

Lessons Learnt

8 Output Schema

Primary Output File

Probability-First Output

9 Technical Appendix

Appendix A: Technical Reference

A.1 Data Dictionaries

Raw Source: student_outcome.parquet

Processed: student_outcome_pat.parquet

Processed: student_outcome_teacher.parquet

A.2 Data Quality Gates

Gate 1a: Data Quality Audit

Gate 1b: Indicator Coherence

Missingness Diagnostics

Cluster Structure

A.3 Mathematical Model Specifications

Single-η Framework

Measurement Model

Risk z-score Conversion (at scoring time only)

Hierarchical Structure

Key Parameters

Frequentist Implementation

Appendix B: Diagnostic Detail

B.1 Bootstrap Reliability Analysis

Methodology

Results Summary

Interpretation

Session Information

Raw Source: `student_outcome.parquet`

Processed: `student_outcome_pat.parquet`

Processed: `student_outcome_teacher.parquet`